メーカー、工場における開発研究職、設計職における基礎的なお話。新入社員・中堅社員の参考に。
×
[PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。
このステップでは、解決する問題を明確にし、改善の程度を定めます。
そのためには、まず「データを収集する」必要があります。
その後、取り上げるための「問題を明確化」し、「改善の目標」を設定します。
データの収集は数字である必要があります。
初期不良件数14件など、数値で把握することで、現状を確認できます。
もちろん言語データも重要です。
例えば、「温度上昇による設備の一時停止」という問題の場合、収集できる言語データは、「冷却不足」「過剰電流」などがあります。
この段階では、事実を整理し、思考をまとめるのに役立ちます。しかし数字に比べて、主観的なので情報なので、最終的には、設備の表面温度など数字データ分析することになります。
数字データは2種類に別れます。
1. 計量値
測定器によって得られるデータであり、質量、長さ、角度、速度、電圧、連続して得られる値をとるデータです。
1.66や1.1522など無数に値が存在するため、有効桁数に注意する必要があります。
2. 計数値
数えることで得られるデータです。不適合数、傷の数、汚れなど断続的な数字です。
またそれは計画的に収集する必要があります。
5W1Hが基本となります。
・What:何のデータ?
・Why:何のため?
・Who:誰がデータを?
・When:いつデータ収集する?
・Where:どこでデータを?
・How:どのようにして?
計画の段階では、「偏り無く」「必要な数量」「必要なものだけ」を収集することに注意します。
PR
品質管理では品質問題を解決するために、定められた手順と適切な方法が存在する。
QCストーリは品質の問題を解決するための、代表的な手法である。
手順は
1、現状の把握 ・・・テーマの設定
2、要因の解析 ・・・原因を掘り下げる
3、対策の立案 ・・・原因解決の方法を検討します
4、対策の実施 ・・・対策を実施しますが、ダレが、ドコで?といった計画が重要です
5、効果の確認 ・・・思うように効果があるか確認します。無ければ再検討です。
6、歯止め ・・・効果を確認したら、再発を防ぐべく歯止めをかけます。
の順に行っていく
QCストーリは品質の問題を解決するための、代表的な手法である。
手順は
1、現状の把握 ・・・テーマの設定
2、要因の解析 ・・・原因を掘り下げる
3、対策の立案 ・・・原因解決の方法を検討します
4、対策の実施 ・・・対策を実施しますが、ダレが、ドコで?といった計画が重要です
5、効果の確認 ・・・思うように効果があるか確認します。無ければ再検討です。
6、歯止め ・・・効果を確認したら、再発を防ぐべく歯止めをかけます。
の順に行っていく
測定が正しく行われた上で、偶然に起こりうる測定ごとにばらつく誤差のことを偶然誤差という。
同一条件のもとで、他数回の測定が繰り返されたときに生じる誤差は、正負同等の確率で起こる。
また小さい誤差が起こる確率は高く、大きな誤差は起こりづらい。
偶然誤差は毎回ランダムな値をとるので測定後に取り除くことができない。
ある測定における測定値に、同じ方法を用いて測定する限り、「真の値」にたいして系統的にずれて測定されるような誤差が存在する場合、それを系統誤差と呼ぶ。
測定において過失が無いが、測定器自体のバラつき、経時変化などにおける実験条件のバラつきによって起こる。
これは測定器の校正である程度除外できる。
実験とは、仮説や、理論が実際に当てはまるかどうかを確認すること、また不確定な現象を観測することである。そのため、実験を行うに辺り、"何を明らかにしようとするのか"その目的をはっきりさせる必要がある。これは実験目的を設定する基本である。
実験に対する最も基本的姿勢は、目的を達する積極性である。
また、ある実験が正しいかどうかを確かめることを追試という。
実験に対する最も基本的姿勢は、目的を達する積極性である。
また、ある実験が正しいかどうかを確かめることを追試という。
測定によって得られた値は、ある程度の測定精度をもつ。そのことから値はある範囲でバラつく。一般的にはその平均値を得ることで、もっとも確からしい値(最確値)として判断する。しかし実際の真の値は、最確値と異なり、バラつきの範囲内の中に存在するとしかわからない。このバラつきの範囲を誤差と呼ぶ。
| ↓平均 |
|| | | | | | | | | |||
|← バラつき →|
この間に 真の値が存在する。
ある物理量を測定する場合、使用する測定器がもつ最小測定可能量(最小目盛り)として、感度が定められてる。感度は分解能といわれることもある。言い換えればこの値を下回る測定値の差は、意味をなさないとされる量のことである。
一般的に、測定の精度とは、誤差の割合の最大値を示すもので、測定する物理量の値と、測定器感度の比の絶対値で与えられる。
精度=|測定感度/測定物理量の値|x100
絶対値を用いるのは、本来、正と負の誤差確率が等しいためである。
測定した物理量は、測定器の目盛りによって得られる桁まで有効である。
もし、それぞれの測定器の最小目盛りの間を判読すれば、その最後の桁は誤差が含まれる。
一般的に、測定値は使用した測定器の最小目盛りの1/10まで有効数字として扱う。
ゆえに実験結果の有効数字は、その最終桁に誤差が含まれてることを前提とする場合がある。
精度誤差に記述が無い場合は注意する必要がある。
もし、それぞれの測定器の最小目盛りの間を判読すれば、その最後の桁は誤差が含まれる。
一般的に、測定値は使用した測定器の最小目盛りの1/10まで有効数字として扱う。
ゆえに実験結果の有効数字は、その最終桁に誤差が含まれてることを前提とする場合がある。
精度誤差に記述が無い場合は注意する必要がある。
国際単位系 (SI;フランス語のsyste`me internationalの頭字語) では7つの基本単位が定められている。これをSI基本単位という。これらの基本単位はSIの前身であるメートル法において、一つの量に対して数ある大きさの単位が存在する状況から、一つの量に対して一つの単位に一本化する、という事を目的として選ばれたものである。
SI基本単位は操作的定義 (operational definition) によって定義されている。SI基本単位はSI単位の基本となる単位であり、他の単位(SI組立単位)は、全てSI基本単位(および他のSI組立単位)の組み合わせにより定義される。次元解析により、全てのSI単位はSI基本単位の組み合わせにより表現することができる。
SI基本単位は、以下の7つである。これらの単位は、次元的に独立している。
| 物理 量 | 単位 | |
| 長さ | メートル (m) | 1秒の299 792 458分の1の時間(約3億分の1秒)に光が真空中を伝わる距離として定義されている。 |
| 質量 | キログラム (kg) | 由来は由来 最大密度温度での1 Lの水の質量だが、現在は国際キログラム原器の質量とする |
| 時間 | 秒 (s) | セシウム133の原子の基底状態の2つの超微細準位の間の遷移に対応する放射の周期の9 192 631 770倍に等しい時間 |
| 電流 | アンペア (A) | 真空中に1メートルの間隔で平行に置かれた無限に小さい円形の断面を有する無限に長い2本の直線状導体のそれぞれを流れ、これらの導体の1メートルにつき千万分の2ニュートンの力を及ぼし合う直流の電流 |
| 温度 | ケルビン (K) | 水の三重点の熱力学温度の273.16分の1 |
| 光度 | カンデラ (cd) | 放射強度683分の1ワット毎ステラジアンで540テラヘルツの単色光を放射する光源のその放射の方向における光度 |
| 物質量 | モル (mol) | 0.012キログラムの炭素12の中に存在する原子の数と等しい数の要素粒子又は要素粒子の集合体(組成が明確にされたものに限る)で構成された系の物質量 |
測定とは基準となるものの比較で行われる。
例えば、物体の長さを測定する場合はものさしが必要となる。
ものさしとは、ある基準の目盛りが振ってある。これをあてがう事で、基準長の倍数を読み取れる。
電流計、電圧計も同様に比較用の目盛りがついている。
尚、この目盛りは有限である。決して無限に細かくつけることができない。デジタルにおいても有限である。つまり、このことは測定値は、必ず有限な桁数をもつことを意味する。
37.564cmの長さの物体があるとする。
1mm単位で目盛りがついたものさしで計るとすると、その測定値は37.56cmまでが、測定の限界であり、それ以下の値は測定不可能となる。よって同じものさしで同じ物体を測定した場合、同様の測定値となる。これを"再現性"という。
しかし、同条件で、同じ結果というのは理想である。
ただ一度の測定で、その測定値を信頼できるだろうか?
たとえば観測点の違いにより、対象点の方向が異なる。これを視差という。
このため、測定器および目の位置によっては値が値がことなる。
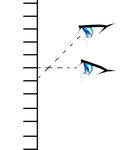 そのため、何回か測定を繰り返し、値の確からしさを定める必要がある。
そのため、何回か測定を繰り返し、値の確からしさを定める必要がある。
つまり誤差を考慮して、測定値は処理されなければならない。
例えば、物体の長さを測定する場合はものさしが必要となる。
ものさしとは、ある基準の目盛りが振ってある。これをあてがう事で、基準長の倍数を読み取れる。
電流計、電圧計も同様に比較用の目盛りがついている。
尚、この目盛りは有限である。決して無限に細かくつけることができない。デジタルにおいても有限である。つまり、このことは測定値は、必ず有限な桁数をもつことを意味する。
37.564cmの長さの物体があるとする。
1mm単位で目盛りがついたものさしで計るとすると、その測定値は37.56cmまでが、測定の限界であり、それ以下の値は測定不可能となる。よって同じものさしで同じ物体を測定した場合、同様の測定値となる。これを"再現性"という。
しかし、同条件で、同じ結果というのは理想である。
ただ一度の測定で、その測定値を信頼できるだろうか?
たとえば観測点の違いにより、対象点の方向が異なる。これを視差という。
このため、測定器および目の位置によっては値が値がことなる。
つまり誤差を考慮して、測定値は処理されなければならない。
サイト内検索
Google Ad
最新記事
(03/20)
(05/09)
(05/09)
(05/09)
(05/09)
(05/09)
(05/09)
(05/09)
(05/09)
プロフィール
HN:
snaker
性別:
非公開
最古記事
(05/09)
(05/09)
(05/09)
(05/09)
(05/09)
(05/09)
(05/09)
(05/09)
(03/20)
最新コメント
最新トラックバック
P R
